Converting Levels Into XP & Vice Versa
Many games (such as my own Pixel Blacksmith and Blacksmith Slots) contain an XP / level system, where performing actions will reward experience, and eventually new levels. These new levels often unlock new content, or provide currency, so keeping players incentivised without feeling like a “grind” is a tricky balance.
The Solution
First, come up with a basic formula to use for calculating the XP required for a level. The most common by far is (level/x)^y, with x affecting the amount of XP (lower values = more XP required per level), and y being how quickly the required xp per level should increase (higher values = larger gaps between levels).
Next, make a spreadsheet where x and y can be quickly and easily modified, and the XP per level seen. Here is my spreadsheet, feel free to make a copy.
As an example, here’s a comparison of the XP required for levels using varying values of x and y. Note that using 2/3 for y is recommended, so that built in squaring / cubing functions can be used.
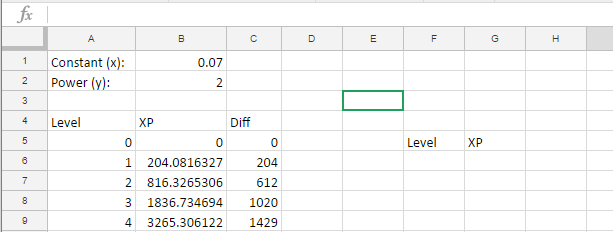
Example 1: X: 0.07, Y: 2
This has a fairly quickly increasing amount of XP per level (y) and a large amount of XP (x), and is good for games where XP is relatively easy to gain.
| Level | XP | Difference |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 204.0816327 | 204 |
| 2 | 816.3265306 | 612 |
| 3 | 1836.734694 | 1020 |
| 4 | 3265.306122 | 1429 |
| 5 | 5102.040816 | 1837 |
| 6 | 7346.938776 | 2245 |
| 7 | 10000 | 2653 |
| 8 | 13061.22449 | 3061 |
| 9 | 16530.61224 | 3469 |
| 10 | 20408.16327 | 3878 |
Example 2: X: 0.3, Y: 2
This has a high value for x, so the amounts of XP required for a level up are very small. This would be good for a game where XP is relatively hard to obtain (e.g. requires collecting items). Note that the % increase in XP between levels 1 and 2 is the same as Example 1 (3x higher).
| Level | XP | Difference |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 11.11111111 | 11 |
| 2 | 44.44444444 | 33 |
| 3 | 100 | 56 |
| 4 | 177.7777778 | 78 |
| 5 | 277.7777778 | 100 |
| 6 | 400 | 122 |
| 7 | 544.4444444 | 144 |
| 8 | 711.1111111 | 167 |
| 9 | 900 | 189 |
| 10 | 1111.111111 | 211 |
Example 3: X: 0.07, Y: 3
This uses a different value for y than the other 2 examples, and as such the XP required rapidly increases. This would be used in a game where higher levels have significantly higher XP gaining potential (e.g. an incremental game).
| Level | XP | Difference |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 2915.451895 | 2915 |
| 2 | 23323.61516 | 20408 |
| 3 | 78717.20117 | 55394 |
| 4 | 186588.9213 | 107872 |
| 5 | 364431.4869 | 177843 |
| 6 | 629737.6093 | 265306 |
| 7 | 1000000 | 370262 |
| 8 | 1492711.37 | 492711 |
| 9 | 2125364.431 | 632653 |
| 10 | 2915451.895 | 790087 |
Using The Formula
Now that we have a formula for XP required for any level (using Example 1: XP = (level/0.07)^2), we also need to know the current level based on XP. Inverting the formula gives us level = 0.07 * √XP. The second formula can be harder to implement due to requiring “nth root of”, hence why using a value of 2/3 is recommended.
XP and levels can now be converted easily and efficiently, without requiring any lengthy formulas. However, how useful the formula will be depends entirely on how well the x and y values are tuned for the specific use case. Get it wrong, and players will power through content or complain about being too grindy, get it right and they’ll never mention it!
The Conclusion
Levels are an extremely common way of rewarding consistent players, and providing an incentive to continue playing the game, or to replay older content. Balancing the formula is extremely important, and the simplicity of the formula described in this post means that consistent complaints of level ups being too frequent or too infrequent can be fixed by changing a single variable.
It is applicable to pretty much any game on any platform, but is especially useful in mobile applications, where processing power can be more limited, and player attention harder to keep.
A gist of a Java implementation of converting between XP & levels, as well as calculating current % progress towards next level is available here.