Calculating Weapon Damage Using Ideal Ranges
Whilst building a turn based strategy shooter, weapons needed to have “ideal ranges”. For example, a melee weapon should only work from 1 tile away, a shotgun should prefer short ranges, a sniper rifle should prefer long ranges, etc. The non-melee weapons should still work outside of their ideal range, but with reduced damage.
The Solution
First, the weapon ranges must be calculated, then whether the target distance is inside this range or not, and finally calculate the total damage based on the previous value.
These are the minimum and maximum ranges for each type of weapon, along with how numbers are included in this range (note that this is an inclusive range, so includes the minimum and maximum values):
| Weapon Type | Minimum | Maximum | Range |
|---|---|---|---|
| Melee | 1 | 1 | 1 |
| Short | 2 | 4 | 3 |
| Medium | 5 | 7 | 3 |
| Long | 8 | 15 | 8 |
For this post a consistent set of test values will be used: 1, 2, 3, 5, 8, and 10 tiles away, providing a range of values that fall in and out of all weapon’s ideal ranges.
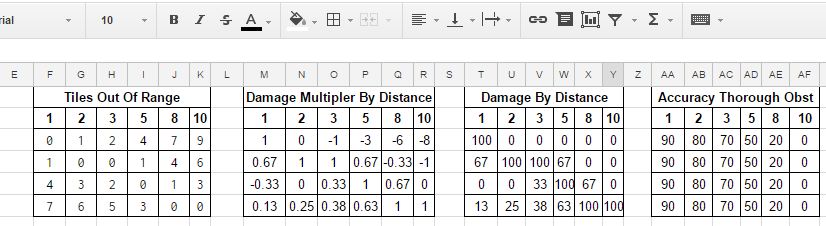
Tiles Out Of Range
First, if our test value is within a weapon’s ideal range, then it is 0 outside of ideal range. Alternatively, get the minimum absolute value of the difference between the value and the minimum and maximum bounds of the range. That was a bit of a mouthful, an example should clarify!
In this example the long weapon type (range 8-15 tiles) will be firing at a target 5 tiles away. 5 is -3 away from the minimum, 8, and -10 away from the maximum, 15. The absolute value of these two is 3 and 10, the minimum of which is 3. Via this rather convoluted process, the fact that the target is 3 tiles out of range is now known.
The below table shows a full matrix of tiles out of range for each weapon type. The example above is shown in red.
| 1 | 2 | 3 | 5 | 8 | 10 | |
|---|---|---|---|---|---|---|
| Melee | 0 | 1 | 2 | 4 | 7 | 9 |
| Short | 1 | 0 | 0 | 1 | 4 | 6 |
| Medium | 4 | 3 | 2 | 0 | 1 | 3 |
| Long | 7 | 6 | 5 | 3 | 0 | 0 |
Damage Multiplier
Next, the damage multiplier will be calculated, based on how far out of ideal range the target is. This is a simpler formula than before, being 1 - (tilesOutOfRange / weaponRange). Using the same example situation as before, the calculation will be 1 - (5 / 8) = 0.375. If a negative damage multiplier is calculated, then 0 will be used instead.
As before, the below table shows a full matrix of damage multiplier for each weapon type based on distance away, with the example highlighted in red. Note that values are rounded to 2 decimal places for visual clarity, so the example becomes 0.38.
| 1 | 2 | 3 | 5 | 8 | 10 | |
|---|---|---|---|---|---|---|
| Melee | 1 | 0 | 0 | 0 | 0 | 0 |
| Short | 0.67 | 1 | 1 | 0.67 | 0 | 0 |
| Medium | 0 | 0 | 0.33 | 1 | 0.67 | 0 |
| Long | 0.13 | 0.25 | 0.38 | 0.63 | 1 | 1 |
Damage
Now, the final step! Simply multiply the weapon’s base damage by the multiplier to calculate the actual weapon damage dealt. For such a basic calculation no table is needed, but if the sample long distance weapon is assumed to deal 100 damage, we end up with the conclusion that the weapon will deal 38 damage to a target 5 tiles away. Melee weapons are also only effective 1 tile away.
Misc
Below I’ve quoted my rough notes for the formula, as a more concise but less clear version of the calculations above:
Weapon Range = (Maximum – Minimum) + 1.
Tiles Out Of Range = If in range, then 0. Otherwise, the minimum (absolute) distance between the tile and the minimum or maximum.
Damage Multiplier = (1 – (Tiles Out Of Range / Weapon Range).
Damage = If damage multiplier > 0, then base damage * damage multiplier, otherwise 0.
Additionally, a Java implementation is available as a Gist, which may be easier to understand.
The Conclusion
Whilst the actual use case is fairly niche, this post should indicate why a generic formula is often the preferred approach instead of hardcoding lookup tables. With the approach taken, adding a new weapon type or dynamically adjusting a weapon’s range is very easy, and the damage is quickly calculated.
The formula may be useful for anyone needing to calculate values that need to drop off outside of a specific range at a varying rate, based on the size of the range.
Additionally, this was a “iteratively created” formula, where I essentially played with variables in Excel / Google Sheets until I got values that matched what I wanted to see. As such, I strongly suspect some steps are inefficient, particularly when calculating how far out of range a target is.